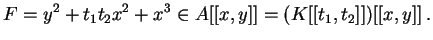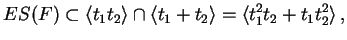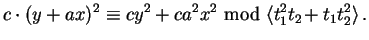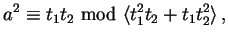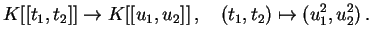|
Equisingular Stratum - in Positive
Characteristic
If char(K) divides the order of some branch of
f, then in general there is no such (strong) equisingular stratum.
|
Example.
|
Let char(K)=2 and consider the deformation of the cusp defined by
The following define (obviously) equisingular deformations
- F mod (t1-t2), since then F = (y +
t1x)2 + x3 ;
- F mod (t1t2)
Now assume that ES(F) would be an equisingular stratum for the
deformation defined by F. Then the 2nd defining property gives
and the first would imply the existence of c, a in
K[[t1,t2]] such that the 2 jet of F equals
But this means
which is impossible.
|
The reason is the existence of weak equisingular
deformations, which become equisingular deformations after a finite
base change, here:
-> Back
|