Lösung des Optimierungsproblems
Man berechne das binomiale Ideal
Im Beispiel:
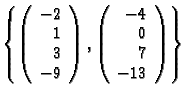 ist eine Basis der Lösungsmenge
ist eine Basis der Lösungsmenge ![]() .
.
Daraus errechnet man
Satz:
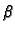 ist optimale Lösung der Aufgabe
ist optimale Lösung der Aufgabe
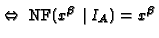 .
.- Wenn
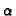 Lösung, i.e.
Lösung, i.e. 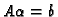 und
und
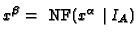 , dann ist
, dann ist 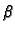 optimale Lösung.
optimale Lösung.
NF bezeichnet die Normalform bzgl. einer Gröbnerbasis für
die Monomenordnung:
![]() oder
oder
![]() und
und
![]() .
.
Im Beispiel:
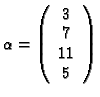
![]()
also
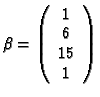
ist eine optimale Lösung.